Những hình vuông vẽ sai                        

Dựng hình và kiểm tra

1. Vẽ một tam giác vuông.

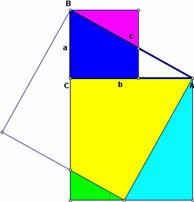
2. Vẽ một hình vuông “sai cách” trên cạnh a, như thế hình vuông đó sẽ nằm chồng lên tam giác, và vẽ một hình vuông trên cạnh b nằm ngoài tam giác.

3. Vẽ một hình vuông :”sai cách” trên cạnh huyền (cạnh c), tức là hình vuông này cũng nằm chồng lên tam giác vuông ABC.

4. Như vậy, hai hình vuông trên cạnh a và cạnh b được chia thành 5 miền riêng biệt. Vẽ các điểm phân cách các miền được tạo ra từ các hình vuông, sau đó vẽ hình đa giác trên các miền này từ những điểm vừa vẽ được ở trên.

5. Quan sát hình bên ta thấy rằng, một trong những mảnh của hình vuông trên cạnh a cũng nằm bên trong hình vuông trên cạnh c, và một mảnh của hình vuông trên cạnh b cũng nằm trong hình vuông trên cạnh c.

- Sử dụng công cụ Translator để tạo ra các bản sao di chuyển được của 3 mảnh này.Sau đó làm ẩn đi các mảnh gốc, và sắp xếp các mảnh bản sao vào hình vuông trên cạnh c sao cho hình được khớp vừa khít.

6. Di chuyển một đỉnh để thay đổi tam giác của bạn, và xếp lai các mảnh để chứng thực các việc làm này với các dạng tam giác khác nhau.

Nhận xét

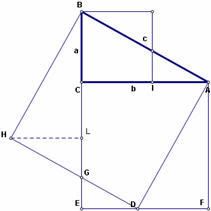
Ví dụ: bên có 3 miền sẽ được di chuyển vào 3 miền đồng dạng với nó , đó là các miền nào? .

- Ta thấy 3 miền di chuyển được và 3 miền mà chúng sẽ chuyển tới đều là tam giác vuôngVì thêa phải chứng minh kích trước của miền di chyển và miền nó sẽ chuyển toái là bằng nhau, bằng cách chỉ cần chứng minh 2 tam giác vuông có 1 cặp cạnh bằng và 1 cặp góc không vuông bằnh nhau .

Sự chứng minh bằng hình vuông nghiêng

Đây là trường hợp, bạn chỉ cần vẽ một hình đơn giản mà bạn có thể dùng để chứng minh được định lí Pitago. Các cách đó là: dùng các hình di chuyển được hoặc dùng một phép tính số học đơn giản để tình toán cách dịch chuyển các hình. Hình vẽ minh họa cho trường hợp này thì xuất hiện trong các văn bản từ rất xa xưa, và thậm chí bạn còn thấy chúng trong các kiểu lát trang trí. Nhưng không ai biết rằng, đó có thể là cách để chứng minh định lý Pitago, dường như nó đã được biết tới ở Trung Quốc và Ấn Độ, và học thuyết Pitago đã được nghiên cứu bởi các nhà nghiên cứu Trung Quốc và Ấn Độ ở thời đại Babilonia. Dựng hình và Kiểm tra

1. Vẽ một hình vuông và tâm của hình vuông đó.

2. Vẽ một điểm trên cạnh hình vuông.

3. Đánh dấu vào điểm tâm của hình vuông làm tâm xoay, và xoay điểm đó trên các cạnh bởi một góc 900 . Lặp lại cho đến khi tạo được 4 điểm trên 4 cạnh của hình vuông

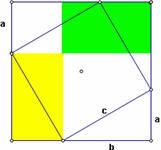
4. Sử dụng các điểm này để vẽ được hình vuông nghiêng nằm trong hình vuông lớn hơn.

5. Tô màu miền trong của các tam giác trên các góc tạo với hình vuông lớn hơn( như hình trên).

6. Nhãn của các cạnh theo thứ tự từ nhỏ đến lớn của tam giác vuông là a,b,c, trong đó c gọi là cạnh huyền.

7. Bây giờ bạn sẽ di chuyển các tam giác vuông ( bằng cách tạo bản sao di chuyển). Hãy sử dụng công cụ Translator để vẽ các bản sao dịch chuyển được của 3 trong 4 miền tam giác, Làm ẩn đi 3 miền tam giác gốc.

8. Sắp xếp lại các tam giác, bạn sẽ có được 2 hình chữ nhật như hình bên.

9. Di chuyển điểm đáy để làm biến đổi hình và vị trí chứa các tam giác để chứng thực các việc làm này đối với các hình tam giác khác.

Nhận xét

Bạn có thể chứng minh định lý bằng phương pháp đại số căn cứ vào cách chứng minh bạn đã làm. Và dưới đây là 1 vài mẹo dơn giản đẻ chứng minh định lý:

1. Chứng minh hình nghiêng ở bên trong là một hùnh vuông, và tính diện tích của nó theo tham số c.

2. Chiều dài của một cạnh của hình vuông lớn hơn bằng bao nhiêu?. Viết một biểu thức để tính diện tích của hình vuông này theo a, b.

3. Tính diện tích của một tam giác vuông và tổng diện tích của 4 tam giác vuông.

4. Viết một biểu thức khác tính diện tích của toàn bộ hình, Sử dụng các số hạng của biểu thức tính diện tích các tam giác và diện tích hình vuông nghiêng.Tức là tính diện tích hình theo 3 số hạng a,b,c.

GV: TRần Anh Tuấn