Gốc > Góc Toán Học >
Một số phương pháp tìm nghiệm nguyên
I, Các công thức về chia hết đáng chú ý:
Nếu và
và  thì
thì  .
.
Nếu và
và  thì
thì 
II, Các tính chất tiêu biểu của số chính phương.
Số chính phương có tận cùng là .
.
Số chính phương chia hết cho thì chia hết
thì chia hết 

Tích 2 số nguyên liên tiếp là 1 số chính phương thì 1 trong 2 số nguyên đó bằng 0.
Nếu 2 số nguyên có UCLN là 1 và có tích là 1 số chính phương thì mỗi số đó đều chính phương.
Số chính phương chia 3 dư 0,1. Số chính phương lẻ chia 4 hay 8 đều dư 1.
III, Các phương pháp giải PTNN:
1, Đưa về PT ước số:
VD 1: Giải PTNN sau: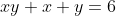 .
.
Giải: . Vậy
. Vậy  . Thay vào tìm
. Thay vào tìm  .
.
Lưu ý, nếu ta đưa được về dạng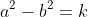 thì để rút bớt các TH, người ta thường đưa về
thì để rút bớt các TH, người ta thường đưa về  khi đó với nhận xét:
khi đó với nhận xét: 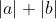 và
và  cùng tính chẵn lẻ, ... ta sẽ rút bớt TH xảy ra.
cùng tính chẵn lẻ, ... ta sẽ rút bớt TH xảy ra.
2,Tách giá trị nguyên :
VD 2: Giải PTNN: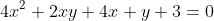 .
.
Giải:
Nên y nguyên khi . Thay vào tìm
. Thay vào tìm 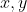 .
.
3,Sử dụng biệt thức Delta ( ).
).
VD 3:Giải PTNN :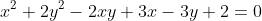 .
.
Giải: .
.
PT có nghiệm khi

Nên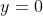 . Thay vào tìm
. Thay vào tìm  .
.
Trong nhiều TH ta lại ko xét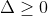 mà ta xét : PT có nghiệm nguyên khi
mà ta xét : PT có nghiệm nguyên khi  là số chính phương.Rồi đưa về PT ước số.
là số chính phương.Rồi đưa về PT ước số.
VD 4: Giải PTNN: .
.
Giải:
Xét : . Phương trình có nghiệm nguyên khi
. Phương trình có nghiệm nguyên khi  là số chính phương.Hay:
là số chính phương.Hay: 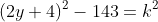
 . Đây ;là PT ước số, ta dễ tìm đựoc GT của
. Đây ;là PT ước số, ta dễ tìm đựoc GT của  rồi tìm
rồi tìm  .
.
4,Đưa về tổng các bình phương.
VD 4: Giải PTNN :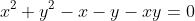 .
.
Giải:

Xét các TH rồi tìm ra x,y.
5,Sử dụng tính chất về chẵn lẻ, chia hết.
VD 5: Giải PTNN :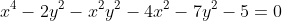 .
.
Giải: .
.
 lẻ, nên
lẻ, nên 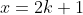 . Thay vào:
. Thay vào:

 chẵn nên
chẵn nên 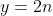 . Lại thay vào:
. Lại thay vào:
 ( vô lí vì VT là số chẵn, VP là số lẻ).
( vô lí vì VT là số chẵn, VP là số lẻ).
Vậy PT vô nghiệm nguyên.
6,Sử dụng dạng phân tích của liên phân số: .
VD 6: Giải PTNN: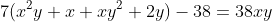 .
.
Giải:
Vì đây là dạng phân tích duy nhất của nên
nên 
Trần Anh Tuấn @ 20:13 18/12/2009
Số lượt xem: 425
Nếu
Nếu
II, Các tính chất tiêu biểu của số chính phương.
Số chính phương có tận cùng là
Số chính phương chia hết cho
Tích 2 số nguyên liên tiếp là 1 số chính phương thì 1 trong 2 số nguyên đó bằng 0.
Nếu 2 số nguyên có UCLN là 1 và có tích là 1 số chính phương thì mỗi số đó đều chính phương.
Số chính phương chia 3 dư 0,1. Số chính phương lẻ chia 4 hay 8 đều dư 1.
III, Các phương pháp giải PTNN:
1, Đưa về PT ước số:
VD 1: Giải PTNN sau:
Giải:
Lưu ý, nếu ta đưa được về dạng
2,Tách giá trị nguyên :
VD 2: Giải PTNN:
Giải:
Nên y nguyên khi
3,Sử dụng biệt thức Delta (
VD 3:Giải PTNN :
Giải:
PT có nghiệm khi
Nên
Trong nhiều TH ta lại ko xét
VD 4: Giải PTNN:
Giải:
Xét :
4,Đưa về tổng các bình phương.
VD 4: Giải PTNN :
Giải:
Xét các TH rồi tìm ra x,y.
5,Sử dụng tính chất về chẵn lẻ, chia hết.
VD 5: Giải PTNN :
Giải:
Vậy PT vô nghiệm nguyên.
6,Sử dụng dạng phân tích của liên phân số: .
VD 6: Giải PTNN:
Giải:
Vì đây là dạng phân tích duy nhất của
Trần Anh Tuấn @ 20:13 18/12/2009
Số lượt xem: 425
Số lượt thích:
0 người



























Các ý kiến mới nhất